
Jouez aux puzzles en ligne à Futoshiki
Dans le tutoriel suivant, les techniques de base et avancées pour résoudre des puzzles Futoshiki sont présentées étape par étape, avec des illustrations accompagnant pour montrer les méthodes sur des configurations de carte spécifiques.
Le point de départ pour parvenir à une solution est la définition du jeu lui-même : Futoshiki demande à l'utilisateur de trouver une planche où chaque chiffre apparaît une fois sur chaque rangée et colonne, en respectant les inégalités des planches. L'utilisation de ce critère permet de progresser vers une solution en remplissant, étape par étape, des carrés vides avec des chiffres spécifiques car ils sont le seul moyen de respecter les restrictions des planches.
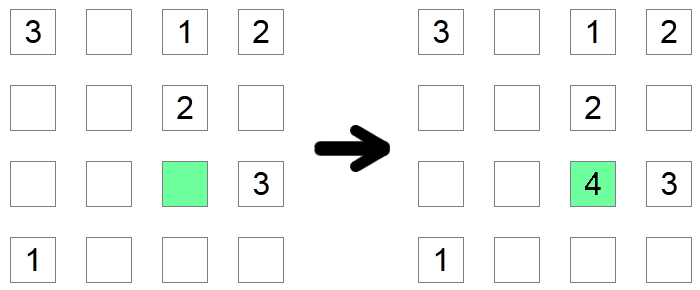
Si une colonne et une ligne de carrés contiennent déjà tous les chiffres possibles, sauf un, alors ce carré doit contenir le chiffre manquant. Dans l'exemple ci-dessus, le carré vert doit être 4 car il ne serait pas autorisé à avoir d'autres valeurs car les autres chiffres possibles se trouvent déjà dans sa ligne ou sa colonne.
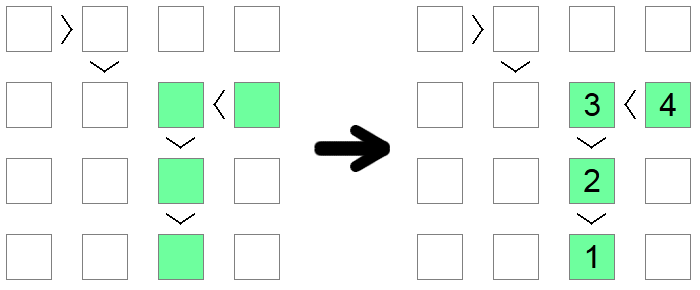
Si vous remarquez une chaîne d'inégalités, que ce soit < (toutes ascendantes) ou > (toutes descendantes), de taille égale à la taille des planches, alors cette chaîne doit être une séquence comprise entre 1 et la longueur de la planche. La longueur de la chaîne garantit que cette séquence est la seule solution possible qui satisfait la condition monotone imposée par la chaîne d'inégalité.
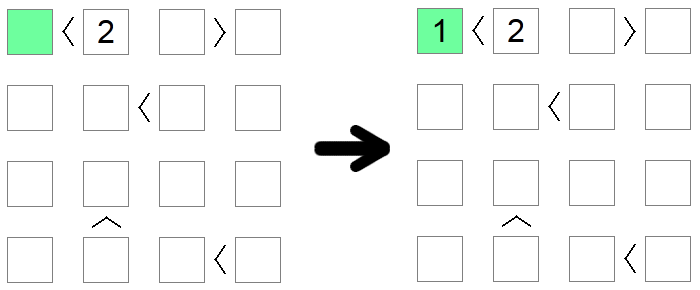
Les carrés inférieurs à 2 doivent implicitement avoir la valeur 1 , car il s'agit de la seule valeur admissible sur la carte qui respecte cette condition. De même, les carrés qui sont supérieurs à la taille de la carte moins 1 doivent être égaux à la taille de la carte. Dans l'exemple ci-dessus, la seule valeur possible pour le carré vert (moins de 2) est 1.
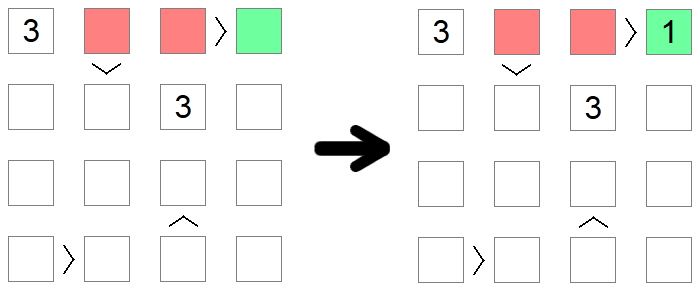
Les carrés supérieurs aux autres carrés ne peuvent pas être 1, la valeur la plus basse autorisée sur le tableau, car aucune valeur n'est inférieure à 1. De même, les carrés inférieurs aux autres carrés ne peuvent pas contenir la valeur maximale autorisée, car il n'y aurait rien de plus grand à remplir de l'autre côté de l'inégalité. Dans l'exemple ci-dessus, 1 ne peut pas être rempli dans les carrés rouges car ils sont tous plus grands que les autres carrés de planche, de sorte que le seul placement possible pour 1 sur la première rangée de la planche est le carré vert.
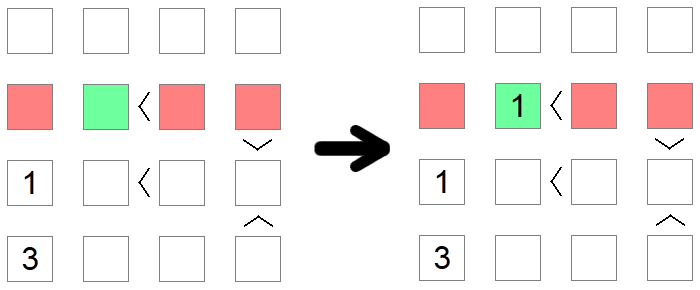
Parfois, plusieurs règles doivent être utilisées pour parvenir à une conclusion. C'est le cas dans l'exemple ci-dessus, où nous essayons de placer la valeur 1 sur la deuxième rangée de la carte. Le premier carré rouge est éliminé en raison d'une exclusion de colonne (nous avons déjà un 1 sur cette colonne), tandis que les deuxième et troisième carrés rouges sont éliminés en raison d'une exclusion des valeurs min car ces endroits ont des inégalités plus grandes que les inégalités qui y sont associées. Par conséquent, le carré vert reste le seul endroit possible pour placer 1 dans cette rangée.
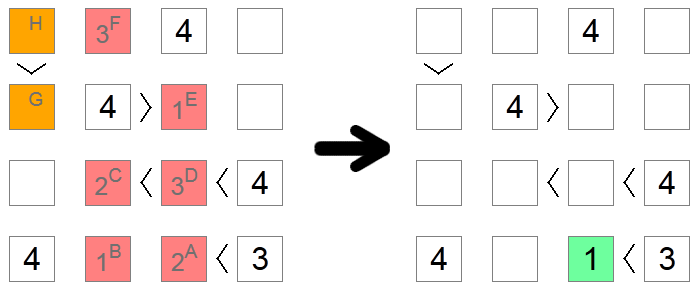
Parfois, surtout sur les planches difficiles, il n'y a pas d'autres moyens de déterminer le chiffre correct pour un carré, sauf pour plonger dans les implications de chaque possibilité jusqu'à ce qu'une contradiction soit atteinte. Dans l'exemple ci-dessus, tous les carrés rouges et orange sont initialement vides. Nous voulons savoir si le carré A contient 1 ou 2 . Nous supposons qu'il contient 2 et nous vérifions si nous arrivons à une contradiction basée sur cette hypothèse.
Si le carré A a un 2, alors le carré B aurait un 1(la seule valeur restante sur la rangée du bas). Carré C peut être 1 ou 2 car il a une chaîne d'inégalités qui nécessite d'avoir disponible 2 nombres plus grands, mais maintenant il ne peut pas être 1 en raison de l'exclusion de la colonne du carré B, donc le carré C est un 2 , et le carré D est un 3 (la seule valeur comprise entre 2 et 4). En raison des exclusions des colonnes, le carré E est 1 et le carré F est 3 .
Maintenant, si nous regardons les carrés orange, nous remarquons la contradiction: si le carré G devait être 2, le carré H devrait être soit 3ou 4, ce qui ne sont pas autorisés en raison d'une exclusion de ligne. Si le carré G devait être 3, le carré H devrait être 4, ce qui n'est pas autorisé pour la même raison. Comme nous n'avons plus de valeurs restantes pour le carré G, cela signifie que nous avons atteint une impasse et que notre hypothèse initiale était fausse: 2 n'est pas un mouvement valide pour le carré A, donc nous pouvons aller de l'avant et y placer 1, la seule autre valeur possible.
Nous avons montré ci-dessus comment résoudre un puzzle Futoshiki avec succès en couvrant une gamme de techniques qui peuvent vous aider à déduire le prochain coup même dans des situations difficiles. L'autre ingrédient clé pour devenir compétent et rapide à résoudre des puzzles Futoshiki est l'expérience: plus vous pratiquez, plus vous deviendrez meilleur et rapide.
Si vous êtes en place pour un défi, vous pouvez jouer dès maintenant un puzzle Futoshiki aléatoire en cliquant sur le bouton ci-dessous. Bonne chance!
© 2026 - Tous droits réservés - À propos - Politique de confidentialité - DE | EN | ES | FR | IT | LT | LV | NL | PL | PT | RO | SV | TR